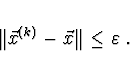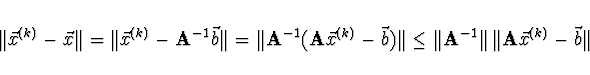

Next: Prostá iterace
Up: Iterační metody řešení soustav
Previous: Příklad nestacionární iterační metody
Pro všechna vlastní čísla 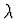 matice
matice 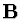 ( tedy čísla, pro která existuje takový
( tedy čísla, pro která existuje takový 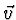 , že
platí
, že
platí
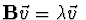 )
musí platit
)
musí platit
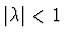 .
.
Věta Nutnou a postačující podmínkou konvergence metody je
podmínka, aby spektrální poloměr
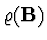 byl
byl
Věta Pokud v některé maticové normě platí
pak iterace konverguje.
Odhad chyby Chceme dosáhnout
přesnosti 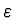 a tedy iterovat, dokud nebude
a tedy iterovat, dokud nebude
Výraz
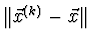 lze odhadnout
lze odhadnout
Jiri Limpouch
2000-03-08
![]() byl
byl
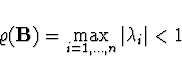
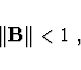
![]() a tedy iterovat, dokud nebude
a tedy iterovat, dokud nebude