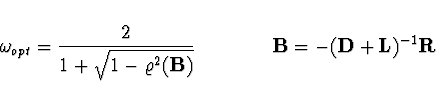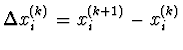 rozdíl mezi
iteracemi Gauss-Seidelovou metodou,
pak je superrelaxační metoda dána vztahem
rozdíl mezi
iteracemi Gauss-Seidelovou metodou,
pak je superrelaxační metoda dána vztahem
Gauss-Seidelovy metoda konverguje pro poměrně širokou třídu matic,
ale její konvergence může být velmi pomalá. Označíme-li
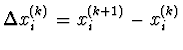 rozdíl mezi
iteracemi Gauss-Seidelovou metodou,
pak je superrelaxační metoda dána vztahem
rozdíl mezi
iteracemi Gauss-Seidelovou metodou,
pak je superrelaxační metoda dána vztahem
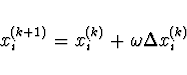
Relaxační faktor slouží
k urychlení konvergence metody a jeho optimální hodnotu lze
vypočítat ze vztahu