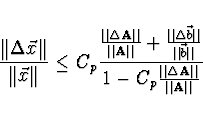

Next: Výpočet inverzní matice a
Up: Přímé metody řešení soustav
Previous: Iterativní zpřesnění řešení
Vzhledem k chybám vstupních údajů a zaokrouhlení
místo
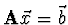 řešíme úlohu
řešíme úlohu
Nejdříve případ
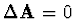
Pro relativní chybu řešení tedy platí
Číslo
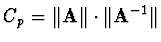 se nazývá
podmíněnost matice.
se nazývá
podmíněnost matice.
Pokud je i
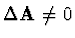 , pak
, pak
Pro 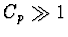 je soustava špatně podmíněná a malé chyby vstupních dat
i malé zaokrouhlovací chyby ve výpočtu se projeví velkou chybou řešení.
je soustava špatně podmíněná a malé chyby vstupních dat
i malé zaokrouhlovací chyby ve výpočtu se projeví velkou chybou řešení.
Jiri Limpouch
2000-03-08
![]() řešíme úlohu
řešíme úlohu
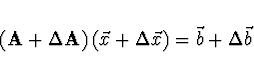
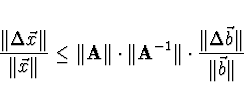
![]() , pak
, pak