Parabolická interpolace

Předpokládejme, že minimum je ohraničené $a < b < c$ a $f(a) > f(b) < f(c)$. Označme $\delta x = x - b$, pak v okolí $b$ lze psát $f(x) \approx \alpha (\delta x)^2 + \beta (\delta x) + \gamma$. V minimu je nulová derivace

$$0 = \frac{{\rm d}f}{{\rm d}x} \approx \alpha (\delta x) + \b... ...ad \Rightarrow \quad \delta x = - \frac{\beta}{2 \alpha} \ \ .$$

Nyní odvodíme hodnoty $\alpha$, $\beta$ pomocí interpolace Lagrangeovým kvadratickým polynomem. Definujeme-li $X = x - b$, $A = a - b$ a $C = c - b$, lze zapsat

$$f(x) \approx \frac{X (X - C)}{A (A - C)} f(A) + \frac{X (X - A)}{C (C - A)} f(C) + \frac{(x - A) (x - C)}{A\, C} f(B) \ \ .$$

Potom jsou $\alpha$ a $\beta$ dány vztahy

$$\alpha = \frac{-A (f(B) - f(C)) + C(f(B) - f(A))}{A\, C (C - A)}$$

$$\beta = \frac{A^2 (f(B) - f(C)) - C^2 (f(B) - f(A))}{A\, C (C - A)} \ \ .$$

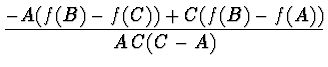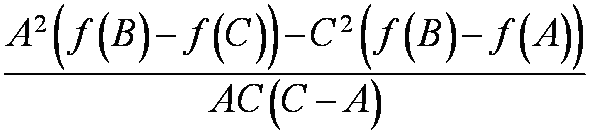Odhadem minima je tedy $x$ dané vztahem

$$x = b - \frac{1}{2} \frac{(b-a)^2 [f(b) - f(c)] - (b-c)^2 [f(b) - f(a)]}{(b-a) [f(b) - f(c)] - (b-c) [f(b) - f(a)]}\ \ .$$

Tato metoda, pokud není doplněna sledováním ohraničení minima, může selhat - nemusí konvergovat nebo může nalézt maximum místo minima.

Je to kvadratická metoda $\rightarrow$ může být neefektivní daleko od minima $\Rightarrow$
přepínání mezi parabolickou interpolací a metodou zlatého řezu.

Pozn. Autorem algoritmu přepínání R. P. Brent. Nutné je sofistikované uchovávání mezivýsledků (bookkeeping).